Calculus Calculator, AI, Calculus Formula Derivatives and Integrals

Calculus calculator derivatives and integrals

Helooo Engpocket friends, if you are an engineer, you must know that nothing stays static. Temperatures fluctuate, changing speeds, or structures vibrate. How to understand these changes? We can use calculus! Whether to analyzed cooling rate of an HVAC system or the stress on a pipe.

To help you calculate calculus faster, this calculus calculator helps you compute the rate of change (Derivative) and the accumulation of quantities (Integral).

Calculus formulas

$\begin{array}{l} \textbf{Derivative} \\ \text{Formula: } \frac{d}{dx}(x^n) = nx^{n-1} \\[10pt] \text{Example: } \frac{d}{dx}(x^3) = 3x^2 \\[25pt] \textbf{Integral} \\ \text{Formula: } \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \\[10pt] \text{Example: } \int x^2 \, dx = \frac{x^3}{3} + C \\[25pt] \textbf{Product Rule} \\ \text{Formula: } (uv)' = u'v + uv' \\[10pt] \text{Used when multiplying two functions.} \\[25pt] \textbf{Quotient Rule} \\ \text{Formula: } \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2} \end{array}$

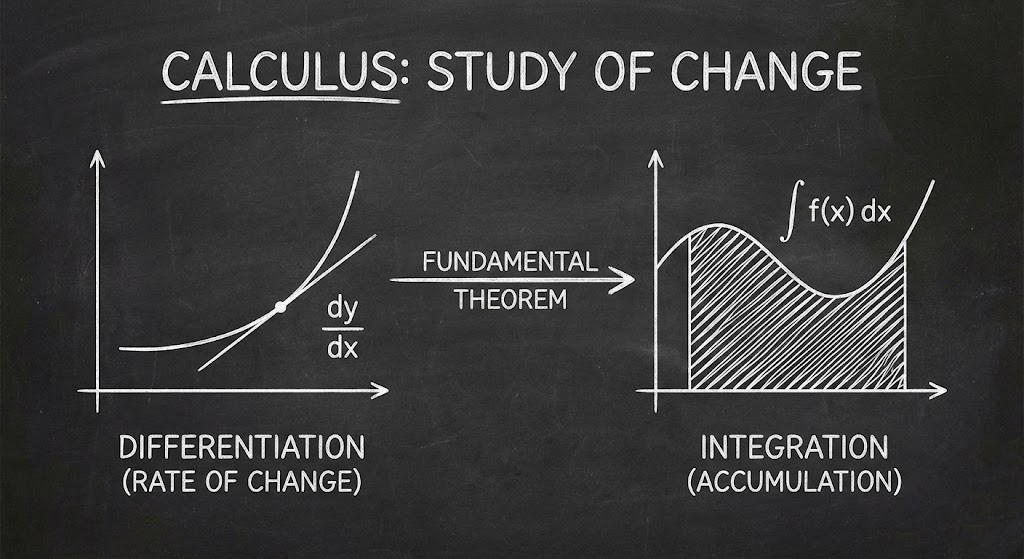
What is calculus?

Calculus is math study of continuous change. It is divided into two types:

1. Differential calculus (Derivatives): Measures how instantly something changes, for example how fast a car is moving at a specific second.
2. Integral Calculus (Integrals): Measures accumulation, for example the total distance walked or how much a volume of a water tank.

As engineers, we also use calculus to calculate something like:
A. Calculating the rate of heat loss through a wall over time (Derivative) to choose an Aircon capacity.
B. Determining the bending moment of a beam (Integral of the shear force).
C. Calculating voltage across a capacitor based on the current flow (Integral).

Example case of calculus

This is the example of manual calculus calculating. You can also try the calculus calculator to make sure that both methods were right and the calculus calculator was accurate.

$\begin{array}{l} \textbf{Example 1: Finding Velocity (Derivative)} \\ \text{Position function: } s(t) = t^2 + 4t \\ \text{Find velocity } v(t) \text{ at } t = 3. \\[10pt] \text{Step 1 (Derive): } v(t) = s'(t) = 2t + 4 \\[10pt] \text{Step 2 (Substitute): } v(3) = 2(3) + 4 \\[10pt] \text{Result: } 10 \text{ m/s} \\[30pt] \textbf{Example 2: Area Under Curve (Definite Integral)} \\ \text{Function: } f(x) = 2x \\ \text{Calculate area from } x=0 \text{ to } x=4. \\[10pt] \text{Step 1 (Integrate): } \int 2x \, dx = x^2 \\[10pt] \text{Step 2 (Evaluate): } [4^2] - [0^2] \\[10pt] \text{Result: } 16 \text{ square units} \end{array}$

This is the end of our calculus calculator post. To use our algebra calculator and find about algebra information deeper, you can visit this link.